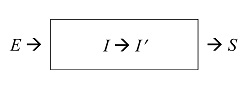GENERADORES

Funciones dinámicas

“Lo que fue nuevo y esencial para toda la matemática fue la concepción enteramente general de función” (Dedekind)


Funciones dinámicas

Las funciones matemáticas (las que utilizan los lenguajes funcionales) se dice que son estáticas (o no mutables), pues siempre devuelven el mismo valor con los mismos argumentos. Por ejemplo, el cuadrado de un número natural, la función coseno de un ángulo, el número de divisores de un número natural, etc. Una constante (por ejemplo 3) se puede considerar una función estática sin argumentos.

Una función dinámica (o mutable) es la que puede devolver un valor diferente con los mismos argumentos. Por ejemplo, una variable (por ejemplo, año) se puede considerar una función dinámica (sin argumentos) que devuelve un valor diferente con el paso del tiempo.

Una función dinámica es una función generalizada en el sentido de que la respuesta S correspondiente a un cierto estímulo E (los argumentos de entrada de la función) depende de su estado interno I, que a su vez cambia (cuando se invoca) a otro estado interno I'.

El esquema es el siguiente:


La máxima generalidad se logra cuando existe polimorfismo, es decir, cuando la función admite además diferentes tipos de entradas, de estados internos y de salidas.

Este modelo es el de los objetos y entidades de la naturaleza. La función estática es un caso particular de un elemento que responde siempre de la misma forma ante el mismo estímulo, independientemente de su posible estado interno. La función estática es un mero concepto matemático que carece de generalidad y que no es aplicable al mundo real.

Este estado interno viene dado por una serie de variables locales persistentes. Puede haber otras variables locales temporales, que no tienen influencia en la respuesta generada.

Un tipo de generador es una función dinámica que devuelve en cada llamada el siguiente elemento de una secuencia.


Especificación en MENTAL

Definición

Una función dinámica (generador) es una función que, al invocarse, puede producir como salida una expresión diferente cada vez. Esto quiere decir que la función depende de variables del entorno que actúan como parámetros internos adicionales.


Ejemplos
  1. Generador g de los elementos a, b y c de forma cíclica. La función g no tiene parámetro formal.

    h=c // parámetro interno de valor inicial c

    (g = ( h=a → (h=b ¡h) )
    ( h=b → (h=c ¡h) )
    ( h=c → (h=a ¡h) )°

    g★5 // eq. (g g g g g) ev. (a b c a b)

  2. Generador de la serie de Fibonacci. Función sin parámetros formales, pero con parámetros internos (n, n1 y n2), con valores inciales nulos.

    (n = 0)
    (n1 = 0)
    (n2 = 0)

    (fibo = ( (n = n+1) ((m = 1) ← (n≥2) →' (m = n1+n2))

    (n1 = n2) (n2 = m) ¡m)° ))

    fibo★5 // ev. (1 1 2 3 5)

  3. Ejemplo con parámetro formal (la función f depende también de la variable m del espacio abstracto):


Inicializar un generador

Si deseamos restaurar un generador para que empiece de nuevo por el primer valor, tenemos que incluir un nuevo parámetro. Por ejemplo, el parámetro k, con dos posibles valores:
  1. k=0 indica inicializar el generador y devolver el primer valor.
  2. k≠0 indica continuar con el generador y devolver el siguiente valor.
Ejemplo para la secuencia de Fibonacci:
Denominación de variables internas

Para evitar que las variables internas de un generador se confundan con las variables externas al mismo, se pueden denominar dichas variables mediante (por ejemplo) expresiones relativas.

Por ejemplo, las variables n, n1 y n2 del generador de los números de Fibonacci se podrían denominar, respectivamente: En virtud del principio de evaluación descendente, aunque existieran valores para n, n1 y n2, siempre se evaluarían primero estas expresiones relativas como variables.


Adenda

Los generadores en los lenguajes de programación

Los generadores se pueden emular con lenguajes tradicionales mediante procedimientos, pero algunos lenguajes los soportan, como Alphard [Shaw, 1981], CLU [Liskov y otros, 1981] e Icon [Griswold, 1983]. La programación con generadores se explica en [Berztiss, 1990] y en [Griswold, 1988].


Bibliografía